terraform automata

Before diving into Terraform Automata, I would like to start with a short introduction about cellular automata and the properties that triggered my fascination with them.

Cellular automata are very simple mathematical models in which cells in a grid evolve based on a set of rules that relate to the state of their neighboring cells.

Their study is the foundation of Stephen Wolfram’s A New Kind of Science, where he demonstrates how complexity arises from simple one-dimensional cellular automata.

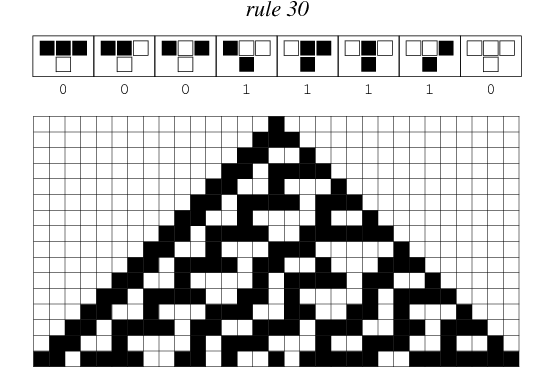
This introduces the concept of computational irreducibility. For some of the simple cellular automata Wolfram studies, such as rule 30 depicted above, the only way of knowing the state of the automaton n generations down the line is to compute all states from n0 to n-1 one by one. Rule 30 is therefore considered computationally irreducible.

Wolfram’s solution to free will and determinism derived from the concept of computational irreducibility resonates with me.

Another remarkable property of simple one-dimensional cellular automata studied by Wolfram is that rule 110 is Turing-complete, meaning it can perform any algorithmically solvable calculation.

Rule 110

Finally, cellular automata are beautiful structures present throughout nature, science and art. Their simple rules produce patterns merging structure with randomness in a mesmerizing way. They can be used to model a wide range of systems, from physical processes like fluid flow and crystal growth, to social phenomena like traffic and crowd behavior.

What better canvas than Terraforms to explore cellular automata?

2. Composable Art

The entire HTML of each Terraform Automata, which contains all data and scripts required to run the automata in your browser, is composed inside the Terraform Automata contract on Ethereum.

Composability, the idea that contracts can trustlessly be built upon and interact with existing contracts is something that excites me about crypto. Terraform Automata are built on the shoulders (i.e. the contracts) of some of the most inspiring and ambitious projects I know.

Terraforms

Firstly, Terraforms by Mathcastles. I won't be able to write a sentence encapsulating everything Terraforms are as it wouldn’t do justice to the depth of the artwork brought to life by the Mathcastles duo 113 and xaltgeist. Instead, I recommend the following resources to learn more about Terraforms:

• An Ode to Terraforms by Mico
• The Map is the Territory by Kevin Buist
• Matto’s explainer video:

EthFS

Next, this project uses EthFS, or Ethereum File System, built by frolic. EthFS is “a public, durable on-chain repository with ergonomic, gas-optimized methods for reading and writing files”.

The javascript library p5.js was uploaded to EthFS by the Mathcastles community and is used to render Terraform Automata.

Additionally, the script I wrote to generate the automata is also stored on EthFS. The Terraform Automata contract enables users to run any other p5.js script inside Terraform Automata by uploading it to EthFS. You can find a short guide about this in Upgrades - a playground for your p5.js scripts below.

Terraform Explorer

Finally, I need to mention Terraform Explorer by el-ranye. Terraform Explorer is a beautiful platform to view and interact with Terraforms. While I am not using Terraform Explorer for the onchain HTML, the preview pictures of Terraforms are fetched from Terraform Explorer’s API.

3. Terraform Automata

Terraform Automata transform each Terraform into three types of cellular automata, which in turn produce hundreds of variations each.

Wolfram - One-dimensional Automata

The first mode generates one-dimensional cellular automata, similar to the ones studied by Wolfram. These automata are created row-by-row, with each cell's value determined by the values of the three cells above it. The heightmap of a Terraform is the basis for the starting row of the automaton, making each automaton unique.

Terraform Automata therefore also benefit from the runtime properties of Terraforms: as the Hypercastle decays and Terraforms evolve, each automaton will evolve as well.

To browse through the many rules of each automaton, click on the automaton or press “n” on your keyboard. By pressing “i” or touching the automaton with two fingers, you can open the command interface where the rule that is currently running is described. You can also jump straight to a specific rule by typing it into the input box in this interface. Finally, the speed at which the automaton moves from step to step can be adjusted with the slider in the interface.

Conway - Two-dimensional Automata

The second mode available generates two-dimensional cellular automata. The best known example of a two-dimensional cellular automaton is Conway’s Game of Life.

Two-dimensional cellular automata expand upon the properties of one-dimensional automata, such as the ability to create infinitely recursive automata using the OTCA metapixel (i.e. “small” cells that are themselves cellular automata form “bigger” cells that are cellular automata, which in turn form even “bigger” cellular automata, etc.). You can find a beautiful implementation of this concept by saharan, here.

You can switch to this mode in Terraform Automata by opening the interface and selecting “2D” in the drop-down menu.

A two-dimensional automaton based on parcel 8644.

All rules in this mode are variations of Conway's Game of Life, in which a cell remains unchanged if it has 2 or 3 neighbors with the same state, and changes to another state if it has more or less neighbors sharing its state. A brief description of the current rule can be found at the bottom of the Terraform Automata interface when this mode is opened.

Langton - Turmites

The final mode available in Terraform Automata is an implementation of a turmite. One of the most famous turmites is Langton’s Ant. Instead of a full row or grid of cells being updated based on its neighbors at every step, this cellular automaton is based on one cell (i.e. the ant) moving across the grid and modifying it as it moves.

Straylight Protocol by Paul Seidler is a great onchain multiplayer game based on turmites. Its Patterns page is a great repository of the variety of patterns a turmite can create.

An ant painting parcel 8644 red.

In Terraform Automata, the ant is randomly positioned within a Terraform and moves based on the values of the Terraform’s heightmap. As it moves, it changes the color of every cell it visits. You can change the color of the ant with the color picker in the interface.

Capture your Automata

You can capture stills and 5 second GIFs of your Terraform Automata by pressing “s” for a jpeg and “g” for a GIF.

Upgrades - a playground for your p5.js scripts

The Terraform Automata contract allows for multiplayer opt-in upgrades that are also reversible. These upgrades can be created by any user and can be opted into by each owner of an automaton separately.

The p5.js script containing the logic of the automata can be replaced with any other custom p5.js script, taking advantage of the following Terraform variables:

• heightmap
• zone
• biome
• fontSize
• font

You can visit the Playground to test scripts and commit them to your automata.

This gives you the freedom to use Terraform Automata as a canvas based on Terraforms. A few ideas that could be fun to experiment with:

• Take advantage of p5.js’ WebGL capabilities and create 3d pieces based on Terraforms.
• Take the base Terraform Automata script and expand it with more automata rules. Especially for two-dimensional automata, there is still a lot to be explored.
• Create interactive pieces and games enabling users to interact with Terraforms.

Once the script is ready, it can be uploaded to EthFS. The name of the uploaded script can then be set in the updateScript function within the Terraform Automata contract.

4. Thanks

A big thank you to the entire Mathcastles community for being a daily source of inspiration, knowledge and positivity. I don’t write a lot in the Discord, but I can’t think of a better community at the frontier of the internet. Thank you to 113 and xaltgeist for bringing Terraforms to life. And thank you to all the builders contributing to Terraforms, especially frolic and el-ranye who created some of the building blocks Terraform Automata are built on.

Finally, I want to thank Chinwe for loving me and supporting me in everything I do.